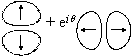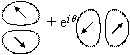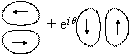Axially symmetric, polarized laser beams
There are many laser beams which can be referred as
axially symmetric, polarized laser beams as shown in Table 1. In this
table, beams are represented by a superposition of a linearly polarized TEM01
and TEM10 modes with orthogonal polarization. By changing the
direction of the polarization and the phase shift, many kinds of axially
symmetric, polarized beams can be obtained. For example, a radially polarized
beam (a) is a superposition of a linearly polarized TEM01 and
TEM10 modes with zero phase shift. When the polarization direction of
the TEM01 and TEM10 mode beams is rotated by 90 degrees,
the beam will be an azimuthally (tangentially) polarized one (i). When
the phase shift is
p, the beams
will be a hybrid mode (c and k). These modes are known as
propagating mode (LP11) in an optical fiber. When the phase shift is
p/2 or 3p/2,
the beam has unique
polarization pattern (b, d, f,
h, j and l). The polarization is basically elliptic and the
ellipticity changes in the azimuthal direction indicating spatial scattering of
the spin angular momentum of light. The beam (e) seems to be be a windmill.
Although the beam (g) resembles a Ninja star, this is the same with the
beams (c) and (k). Note
again that these beams can be generated by a superposition of TEM01
and TEM10 modes with proper polarization and phase shift. Direct
generation from a laser cavity is reported for radially and azimuthally
polarized beams up to date.
Table 1 Examples of axially symmetric, polarized
laser beams.
|
Phase shift
(q) |
0 |
p/2 |
p |
3p/2 |
|
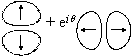 |
a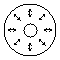 |
b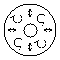 |
c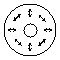 |
d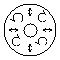 |
|
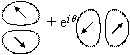 |
e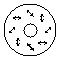 |
f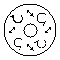 |
g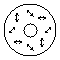 |
h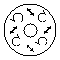 |
|
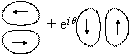 |
i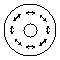 |
j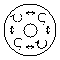 |
k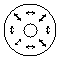 |
l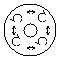 |