Radially polarized laser beams

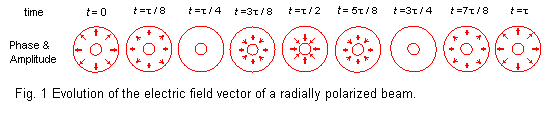
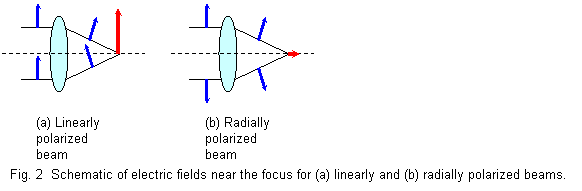
Time evolution of the electric field distribution of a radially polarized beam is shown in Fig. 1. All the electric field vectors have the same amplitude and are arranged with a cylindrical symmetry.  Owing to this nature, the  beam with radial polarization has strong longitudinal component of the electric field near the focus when the beam is strongly focused as shown in Fig. 2.  In addition, the electric filed on the beam axis will disappear because of requirement of the continuity of the electric field, making the beam doughnut-shaped.

However,  if this beam has a spatial variation in phase, this feature will be changed.  For instance, the electric field of the beam with a topological Pancharatnam charge of 1 is depicted in Fig. 3.  In this case, the beam is still radially polarized but the instantaneous distribution of the electric field is no longer cylindrically symmetric.  Moreover, the beam will have an orbital angular momentum.  In other words, the beam has a topological Pancharatnam charge.  Note that there are many kinds of radially polarized beams with different topological Pancharatnam charge.  In addition, the beam may be able to has finite amplitude of the electric field just on the beam axis as shown in Fig. 3 (b) because the continuity of the electric field seems to be secured in one direction.

The above argument will be applicable to azimuthally polarized beams.

Transformation between the radially and azimuthally polarized beams

A radially polarized beam can be transformed to an azimuthally polarized one by using a pair of half-wave plates crossing by an angle of 45 degrees.