radially polarized laser beam (generation)
radially polarized laser beam (calculation)
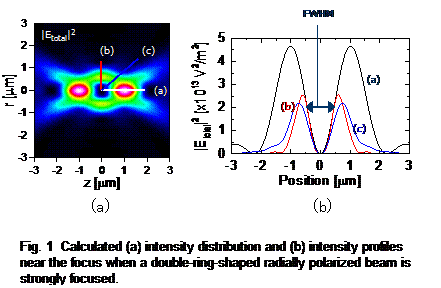
Focusing property of a double-ring-shaped radially polarized beam1,4)
It is known that a strong longitudinal component of electric field appears near the focal point when a laser beam with radial polarization is focused. In addition, we recently indicated that a TM02 mode beam can create a dark region that is surrounded by bright area near the focus1). In this case, the spatial symmetry of the dark region is nearly spherical as shown in Fig. 1 (b). We can call this region an 'optical cage' instead of a 'bottle'. This calculation was done based on the vectorial diffraction theory.
In general, a beam spot with zero intensity at the focus is called dark spot. We numerically found that similar dark spots can be formed by other vector beams with double-ring intensity pattern4).
Sharper focal spot formed by higher-order radially polarized laser beams2)
The intensity distributions near the focal point for radially polarized laser beams including higher-order transverse modes are calculated based on vector diffraction theory. For higher-order radially polarized mode beams as well as a fundamental mode (R-TEM01*) beam, the strong longitudinal component forms a sharper spot at the focal point under a high NA focusing condition. In particular, double-ring-shaped radially polarized mode (R-TEM11*) beams can effectively reduce the focal spot size because of destructive interference between the inner and outer rings with p phase shift. Compared to an R-TEM01* beam focusing in a limit of NA = 1, the full width at half maximum values of the focal spot for an R-TEM11* beam are decreased by 13.6 % for the longitudinal component and 25.8 % for the total intensity.
Calculation of optical trapping forces produced by a radially polarized laser beam3)
Optical trapping technique has widely been used for the precise manipulation of micro- and nano-meter sized particles. When the center of the sphere is on the optical axis, all the rays of a radially polarized beam is p-polarization meaning significant reduction of Fresnel reflection and increase of the optical trapping force. We verified this idea by a simple calculation based on the ray optics. It was confirmed that the trapping force will increase by using a radially polarized beam. In addition, sufficient forces for three dimensional trapping will be obtained even by using an objective with lower numerical aperture and spheres with higher refractive index.
Hollow vortex beams5)
It is well known that a linearly polarized doughnut beam (LG01 mode beam) is not strictly hollow under tight focusing condition. We analytically investigated the conditions under which a beam with spiral phase shift (vortex beam) becomes hollow. By deriving the expressions for the electric fields based on the vector diffraction theory, the value of the topological charge for which the vortex beam is hollow was obtained. This method was applicable to not only axially symmetric polarized beams but also linearly and circularly polarized beams.
Self-healing effect of vector beams7,8)
Scalar Bessel-Gaussian beams are known to have non-diffracting and self-healing effects. We investigated the self-healing effect of vector beams, Bessel- and Laguerre-Gaussian beams at the focal plane under tight focusing condition. Surprisingly, the self-healing effect has been predicted even though half of the input beam at the pupil plane is obstructed, the intensity, phase and polarization distributions were almost the same with that obtained without obstruction for vector Bessel-Gaussian beams7). For vector Laguerre-Gaussian beams, the self-healing effect was also recognized while the effect is lower than that for vector Bessel-Gaussian beams8).
References
1) Y. Kozawa and S. Sato, Focusing property of a double-ring-shaped radially polarized beam, Optics Letters, 31, 820 (2006). link
2) Y. Kozawa and S. Sato, Sharper focal spot formed by higher-order radially polarized laser beams, Journal of Optical Society of America A, 24, 1793 (2007). link
3) H. Kawauchi, K. Yonezawa, Y. Kozawa and S. Sato, Calculation of optical trapping forces on a dielectric sphere in the ray optics regime produced by a radially polarized laser beam, Optics Letters, 32, 1839 (2007). link
4) Y. Kozawa and S. Sato, Dark-spot formation by vector beams, Optics Letters 33, 2326 (2008). link
5) S. Sato and Y. Kozawa, Hollow vortex beams, Journal of Optical Society of America A 26, 142 (2009). link
6) A. Ohtsu, Y. Kozawa and S. Sato, Calculation of second-harmonic wave pattern generated by focused cylindrical vector beams, Appl. Phys. B 98, 851 (2010). link
7) S. Vyas, Y. Kozawa and S. Sato, Self-healing of tightly focused scalar and vector Bessel-Gauss beams at the focal plane, Journal of Optical Society of America A 28, 837 (2011). link
8) S. Vyas, M. Niwa, Y. Kozawa and S. Sato, Diffractive properties of obstructed vector Laguerre-Gaussian beam under tight focusing condition, Journal of Optical Society of America A 28, 1387 (2011). link
9) P. Senthilkumaran, J. Masajada, S. Sato, Interferometry with Vortices, International Journal of Optics, 2012, 517591 (2012). link
10) S. Vyas, M. Niwa, Y. Kozawa, S. Sato, Diffractive properties of obstructed vector Laguerre–Gaussian beam under tight focusing condition, Journal of Optical Society of America A, 28(7),1387 (2011) link
11) S. Vyas, Y. Kozawa, S. Sato, Self-healing of tightly focused scalar and vector Bessel–Gauss beams at the focal plane, Journal of Optical Society of America A, 28(5), 837 (2011) link
12) Y. Kozawa, S. Sato, Focusing of higher-order radially polarized Laguerre-Gaussian beam, Journal of Optical Society of America A, 29(11), 2439 (2012) link
13) S. Vyas Y. Kozawa, S. Sato, Twisted longitudinally polarized field in the focal region, Applied Physics B, 110(1), 7 (2013) link
14) S. Vyas, Y. Kozawa, S. Sato, Polarization singularities in superposition of vector beams, Opt. Express, 21(7), 8972 (2013) link
15) S. Segawa, Y. Kozawa, S. Sato, Resolution enhancement of confocal microscopy by subtraction method with vector beams, Opt. Lett., 39(11), 3118 (2014) link