radially polarized beam (experiment)
radially polarized beam (calculation)
1. ベクトル回折理論による高次径偏光レーザービームの集光特性
近年,ドーナツ形状の強度分布を持った径偏光レーザービーム(TM01)を強く集光すると,焦点付近には電場の軸方向成分だけが現れるというユニークな特性が明らかにされている.我々は,最近二重リング構造の強度分布を持つ高次径方向偏光ビームモード(TM02)の発振を確認しているが,これに関連して高次モードの集光特性について ベクトル回折理論に基づく数値解析を行っている.
径偏光ビームモード(TM0p : p=0,1,・・・)の相対的な電場振幅は,Laguerre-Gaussianモードからの類推により得ることができるので,これよりTM02ビームの伝播に伴う電場や強度分布をベクトル回折理論に基づいて計算することができる.
これまでに,以下のような結果が得られている.
1. 焦点の位置において強度が弱く,逆にその周辺で強度の強い,いわゆるボトルビームとなる強度分布が知られているが1),TM02ビームの場合はさらに対称性がよく, 下図のようにほぼ球対称に近い,”光のかご”状となる.このように焦点での強度がゼロとなるスポットは”ダークスポット”とも呼ばれるが、TM02ビーム以外のビームでも生成されることも明らかにした6)。
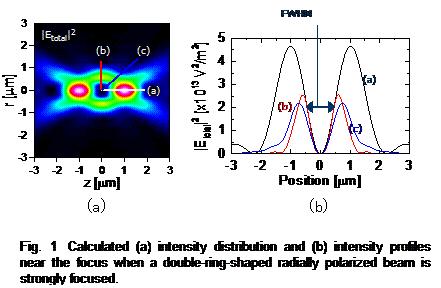
2.集光点での軸方向電場成分が形成するスポット径について,最小で0.40λとなる場合が存在する.これは,これまで報じられていたTM01における軸方向電場成分のスポット径0.45λ2)よりも小さな値であり,TM02モードの強い集光により,さらに小さなスポット径が得られる可能性を示す結果といえる4).
2. 幾何光学に基づく径偏光レーザービームによる光トラッピング力の計算5)
光トラッピングは透明微粒子の非接触かつ精密な捕捉,移動のための強力なツールとして広く利用されている.粒子の中心が光軸上にある場合,径偏光レーザー光は全てp偏光となるため,従来の直線偏光などのレーザービームと比較して,反射の大幅な低減,すなわちトラッピング力の増大が期待される.原理的な検証のため,幾何光学に基づいた光トラッピング力の計算を行った.その結果,光トラッピング力の増大が確認され,(1)小さな開口数のレンズでも,(2)比屈折率が大きい場合でも3次元トラッピングが可能となることが見出された.
3. 完全な中空となる渦ビーム7)
直線偏光のLG01モードビームは、近軸近似では光軸上での光強度がゼロであるが、強く集光すると光軸上でも光強度がゼロとならず、従って、厳密には中空ビームとはならないことが知られている。我々は、螺旋状位相分布を持ついくつかの軸対称偏光ビームに対して、強く集光した場合でも完全に中空になる条件(軌道角運動量あるいはトポロジカルチャージ)をベクトル回折理論に基づいて解析的に求めた。さらに、この手法が直線偏光や円偏光のLaguerre-Gaussianビームにも適用できることを明らかにし、同様に中空ビームとなる条件を求めた。
4. ベクトルビームの自己治癒(Self-healing)効果9,10)
スカラービームのひとつであるBessel-Gaussianビームは、非回折効果と自己治癒効果を持っていることが知られている。どちらの効果も、Bessel-Gaussianビームが、同じ角度で集光される多数のGauss状平面波の重ね合わせと等価であることに由来している。ベクトルビームにもBessel-Gaussian型の強度分布を持つビームが存在することが知られており、我々はベクトルビームを強く集光した場合の焦点付近での自己治癒効果について検討した。その結果、ベクトルBeesel-Gaussianビームでは、スカラーBessel-Gaussianビームよりも高い自己治癒効果を持つことがわかった。特に、瞳面で入射光の半分を覆った場合でも、焦点付近では、覆わなかった場合とほぼ同様の強度、位相、偏光分布を持つことが分かった9)。これは、ベクトルビームが強度、位相、偏光に対して、完全な円筒対称性を持つことに起因していると考えている。ベクトルLaguerre-Gaussianビームの場合にも、やや小さいながら、自己治癒効果が認められた10)。
文献
1) Y. Kozawa and S. Sato, Focusing property of a double-ring-shaped radially polarized beam, Optics Letters, 31, 820 (2006). link
2) S.Quabis et al., Optics Communications 179, 1 (2000).
3) 小澤,佐藤,軸対称偏光ビームの発生法と集光特性,光学, 35 (2006), 625-634 解説記事
4) Y. Kozawa and S. Sato, Sharper focal spot formed by higher-order radially polarized laser beams, Journal of Optical Society of America A, 24, 1793 (2007). link
5) H. Kawauchi, K. Yonezawa, Y. Kozawa and S. Sato, Calculation of optical trapping forces on a dielectric sphere in the ray optics regime produced by a radially polarized laser beam, Optics Letters, 32, 1839 (2007). link
6) Y. Kozawa and S. Sato, Dark-spot formation by vector beams, Optics Letters 33, 2326 (2008). link
7) S. Sato and Y. Kozawa, Hollow vortex beams, Journal of Optical Society of America A 26, 142 (2009). link
8) A. Ohtsu, Y. Kozawa and S. Sato, Calculation of second-harmonic wave pattern generated by focused cylindrical vector beams, Appl. Phys. B 98, 851 (2010). link
9) S. Vyas, Y. Kozawa and S. Sato, Self-healing of tightly focused scalar and vector Bessel-Gauss beams at the focal plane, Journal of Optical Society of America A 28, 837 (2011). link
10) S. Vyas, M. Niwa, Y. Kozawa and S. Sato, Diffractive properties of obstructed vector Laguerre-Gaussian beam under tight focusing condition, Journal of Optical Society of America A 28, 1387 (2011). link
11) P. Senthilkumaran, J. Masajada, S. Sato, Interferometry with Vortices, International Journal of Optics, 2012, 517591 (2012). link
12) S. Vyas, M. Niwa, Y. Kozawa, S. Sato, Diffractive properties of obstructed vector Laguerre–Gaussian beam under tight focusing condition, Journal of Optical Society of America A, 28(7),1387 (2011) link
13) S. Vyas, Y. Kozawa, S. Sato, Self-healing of tightly focused scalar and vector Bessel–Gauss beams at the focal plane, Journal of Optical Society of America A, 28(5), 837 (2011) link
14) Y. Kozawa, S. Sato, Focusing of higher-order radially polarized Laguerre-Gaussian beam, Journal of Optical Society of America A, 29(11), 2439 (2012) link
15) S. Vyas Y. Kozawa, S. Sato, Twisted longitudinally polarized field in the focal region, Applied Physics B, 110(1), 7 (2013) link
16) S. Vyas, Y. Kozawa, S. Sato, Polarization singularities in superposition of vector beams, Opt. Express, 21(7), 8972 (2013) link
17) S. Segawa, Y. Kozawa, S. Sato, Resolution enhancement of confocal microscopy by subtraction method with vector beams, Opt. Lett., 39(11), 3118 (2014) link